บทนิยาม ให้ a และ b เป็นจำนวนเต็ม ไม่ใช่ศูนย์ จำนวนเต็ม ใหญ่สุด d โดยที่ d หาร a ลงตัว และ d หาร b ลงตัว เรียกว่า ตัวหารร่วมมาก ของ a และ b ตัวหารร่วมมากของ a และ b ใช้สัญลักษณ์ gcd(a,b)

ตัวอย่าง ตัวหารร่วมมากของ 24 และ 36 คืออะไร
วิธีทำ ตัวหารร่วมมากของ 24 และ36 คือ 1,2,3,4,6และ 12 ดังนั้น gcd(24,36) =12
ตัวอย่าง ตัวหารร่วมมากของ 17 และ 22 คืออะไร
วิธีทำ จำนวนเต็ม 17 และ22 ไม่มีตัวหารร่วมมากอื่นที่มากกว่า 1 ดังนั้น gcd(17,22)=1

บทนิยาม จำนวนเต็ม a และ b จะเป็นจำนวนเฉพาะ ถ้าเลขสองตัวนี้มีตัวหารร่วมมากเป็น 1

ตัวอย่าง สำหรับตัวอย่างที่แล้วตัวหารร่วมมากของ 17 และ22 เป็นจำนวนเฉพาะ ดังนั้น gcd(17,22)=1

บทนิยาม เลขจำนวนเต็ม a1,a2,a3,…..,an จะเป็นจำนวนเฉพาะต่อกันทีละคู่ ถ้า gcd( ai,aj)=1 เมื่อ 1<=I<j<=n

ตัวอย่าง จงหาจำนวนเต็ม 10,17 และ 21 ที่เป็นจำนวนเฉพาะต่อกันและ จำนวนเต็ม 10,19 และ 24 ที่เป็นจำนวนเฉพาะต่อกัน
วิธีทำ gcd(10,17) = 1 , gcd(10,21) = 1 และ gcd(17,21) = 1 เราสรุปว่า 10,17 และ 21 เป็นจำนวนเฉพาะต่อกันทีละคู่
gcd(10,24) = 2 >1 เราจะเห็นว่า 10,19 และ 24 ไม่เป็น จำนวนเฉพาะต่อกันทีละคู่
อีกวิธีหนึ่งไนการหาตัวหารร่วมมากของเลขสองจำนวนเต็มโดยใช้แฟคตอเรียลขั้นพื้นฐานของเลขสองตัวนี้
แฟคทอเรียลของเลขจำนวนเต็ม a และ b ซึ่งไม่เป็นศูนย์

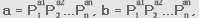
เลขยกกำลังเป็นจำนวนเต็มที่ไม่เป็นลบ และเลข แฟคตอเรียลขั้นพื้นฐานของ a และ b ได้เป็น แฟคตอเรียลที่เลขยกกำลังไม่เป็นศูนย์ ดังนั้น gcd(a,b)จะได้
gcd(a,b) = Pmin(a,b) Pmin(a,b)………… Pmin(a,b)

ตัวอย่าง จงหา แฟคตอเรียลของ 120 และ 500 ซึ่ง 120 =23 * 3*5 และ 500 = 22 * 53
gcd(120,500) = 2min(3,2) 3 min(1,0) 5 min(1,3) = 22 30 5 1 = 20

ทฤษฏี 1 ถ้า a และ b เป็นจำนวนเต็มบวก และจะมีจำนวนเต็ม s และ t อยู่ด้วย ดังนั้น gcd (a,b) = sa + tb

ตัวอย่าง 1 จงแสดงว่าให้เห็นว่า gcd (252,198) = 18
วิธีทำ ให้แสดงว่า gcd (252,198) = 18 อย่างเป็นขั้นตอน
252 = 1*198 + 54
198 = 3*54 + 36
54 = 1*36 +18
36 = 2*18
จากสมการข้างต้น เราสามารถอธิบายได้ว่าส่วนประกอบร่วมของ 252 และ 198 คือ 18 จากคำอธิบายข้างต้นจะเห็นได้ว่า 18 เป็นส่วนประกอบของ 54 และ 36
18 = 54 – 1*36
จากขั้นตอนที่2 บอกเราว่า
36 = 198 – 3*54
จากคำอธิบายข้างต้นจะเห็นได้ว่า ทั้งสองสมการมี 36 เป็นส่วนประกอบร่วม เราสามารถอธิบายได้ว่า 18 เป็นตัวประกอบร่วมของ 54 และ 198
18 = 54 – 1*36 = 54 – 1*( 198 – 3*54 ) = 4*54 – 1*198
จากขั้นตอนที่1 บอกเราว่า
54 = 252 – 1*198
จากสมการข้างต้นจะมี 54 เป็นตัวประกอบร่วม เราสามารถอธิบายได้ว่า 18 เป็นตัวประกอบร่วมของ 252 และ 198 เราสามารถรวมได้ว่า
18 = 4*( 252 – 1*198 ) – 1*198 = 4*252 – 5*198
จบขั้นตอนการทำ

คำอธิบายที่1 ถ้า a, b และ c เป็นจำนวนเต็มบวกและ gcd (a,b) = 1 และ a|bc แล้ว a|c
การพิสูจน์ เนื่องจาก gcd (a,b) = 1 โดยทฤษฏีบทที่1 มีจำนวนเต็ม s และ t ดังนี้
sa + tb = 1
ทำให้สมการทั้งสองข้างเท่ากันโดยการคูณด้วย c ดังนี้
sac + tbc = c
การใช้ทฤษฏีที่1 ของ section 2.4 เราสามารถใช้สมการสุดท้ายนี้แสดงให้เห็นว่า a|c โดยส่วนที่ 2 ของของทฤษฏี, a|tbc เนื่องจาก a|sac และ a|tbc, โดยส่วนที่1 ของทฤษฏี, เราสรุปได้ว่า a หาร
sac + tbc ได้ และดังนั้น a|c จบการพิสูจน์
เราสามารถใช้คำอธิบายที่1 ในการพิสูจน์ของการแยกตัวประกอบในการคูณได้

คำอธิบายที่2 ถ้า p เป็นจำนวนเฉพาะและ 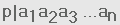ที่ซึ่ง aI เป็นจำนวนเต็ม ดังนั้นp|ai
สำหรับ i บางตัว
เราสามารถแสดงให้เห็นได้ว่าการแยกตัวประกอบของจำนวนเต็มที่อยู่ในจำนวนเฉพาะไม่เท่ากัน นั่นคือ เราจะแสดงให้เห็นได้ว่าจำนวนเต็มหลายๆค่า แยกออกมาได้เป็นจำนวนเฉพาะ นี่เป็นส่วนหนึ่งของพื้นฐานทฤษฏีเลขคณิต
พิสูจน์ เราจะพิสูจน์โดยวิธีหาข้อขัดแย้ง ถ้าจำนวนเต็มบวก n สามารถถูกเขียนออกเป็นจำนวนที่แตกต่างกัน 2ตัวว่า 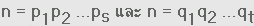บาง pi และ qj เป็นจำนวนเฉพาะที่ซึ่ง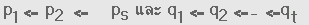
เมื่อเราแทนที่จำนวนเฉพาะทั้งหมดจากการแยกตัวประกอบทั้งสองเราจะได้

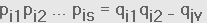
ไม่มีจำนวนเฉพาะเกิดขึ้นของทั้งสองข้างที่เท่ากันและ u และ v เป็นจำนวนเต็มบวก โดยคำอธิบายแสดงให้เห็นว่า pi1 หารด้วย qjkสำหรับ k บางตัว เนื่องจากไม่มีจำนวนเฉพาะหารจำนวนเฉพาะอื่นๆที่ไม่ใช่ตัวมันได้
ดังนั้นคำอธิบายที่1 สามรถใช่พิสูจน์ในการหาผลลัพธ์เกี่ยวกับการหารทั้งสองข้างที่สอดคล้องกันโดยจำนวนเต็มเดียวกัน แสดงว่าเราสามารถคูณทั้งสองข้างที่สอดคล้องกันโดยจำนวนเต็มที่เหมือนกัน อย่างไรก็ตามการหารทั้งสองข้างของจำนวนที่สอดคล้องกัน โดยที่จำนวนเต็มไม่ต้องสร้างจากจำนวนที่สอดคล้องกันก็ได้

ตัวอย่างที่2 14 8 (mod 6) แต่ทั้งสองข้างที่คอนกรูเวน ไม่สามารถหารด้วย 2 ลงตัว เนื่องจาก 14/2 = 7 และ 8/2 = 4 แต่ 7 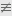4 (mod 6)

ทฤษฎีที่2 ให้ n เป็นจำนวนเต็มบวก และให้ a,b, และ c เป็นจำนวนเต็ม ถ้า ac bc (mod m) และ gcd ( c,m ) = 1 แล้ว a b (mod m)
พิสูจน์ เนื่องจาก ac บ bc (mod m) , m|ac – bc = c( a – b ) โดยคำอธิบาย1 เนื่องจาก gcd ( c,m ) = 1 จะแสดงให้เห็นว่า m|a – b เราสรุปได้ว่า a b (mod m)

GREATEST COMMON DIVISORS AND LEAST COMMON MULTIPLES

the largest integer that divides both of two integers is called the greatest common divisor of these integers.

DEFINITION 4 Let a and b be integers, not both zero. The largest integer d such that d I a and

d I b is called the greatest common divisor of a and b The greatest common divisor
of a and b is denoted by gcd (a, b).
The greatest common divisor of two integers, not both zero, exists because the set of
common divisors of these integers is finite. One way to find the greatest common divisor
of two integers is to find all the positive common divisors of both integers and then take
the largest divisor.this is done in the following examples. Later, a more efficient method
of finding greatest common divisors will be given.

EXAMPLE10 What is the greatest common divisor of 24 and 36?

Solution: The positive common divisors of 24 and 36 are 1, 2, 3, 4, 6, and 12. Hence, gcd(24, 36) = 12.

EXAMPLE11 What is the greatest common divisor of 17 and 22?

Solution: The integers 17 and 22 have no positive common divisors other than 1, so that gcd(17, 22) = 1.

Since it is often important to specify that two integers have no common positive divisor other than 1 we have the following definition.

DEFINITION 5 The integers a and b are relatively prime if their greatest common divisor is 1.

EXAMPLE 12 From Example 11 it follows that the integers 17 and 22 are relatively prime, since

gcd(17, 22) = 1.

Since we often need to specify that no two integers in a set of integers have a common
positive divisor greater than 1, we make Definition 6.

DEFINITION 6 The integers a I, a2 a, are pairwise relatively, prime if gcd(ai, aj = I when-
ever 1 < i < j < no

A

EXAMPLE 13 Determine whether the integers 10, 17, and 21 are pairwise relatively prime and whether
the integers 10, 19, and 24 are pairwise relatively prime.

Solution: Since gcd(10, 17) = 1, gcd(10, 21) 1, and ged( 17, 21) = 1, we conclude that
10, 17, and 21 are pairwise relatively prime.
Since gcd(10, 24) = 2 > 1, we see that 10, 19, and 24 are not pairwise relatively

prime. -4

Another way to find the greatest common divisor of two integers is to use the prime factorizations of these integers. Suppose that the prime factorizations of the integers 42 and b, neither equal to zero, are

a = Pa I pa2 . . . pan, , b = p be I be ... p b ,
1 2 12 1 2 11

where each exponent is a nonnegative integer, and where all primes occurring in the prime factorization of either a or b are included in both factorizations, with zero exponents it necessary. Then gcd(a, b) is given by

gcd(a, b) = pmin(aj, be) p min(a2, be) ... p min (a_
1 2

where mine, yen represents the minimum of the two numbers x and y.'To show that this formula for gcd(a, b) is valid, we must show that the integer on the right-harld side divides both a and b, and that no larger integer also does. This integer does divide both a and b, since the power of each prime in the factorization does not exceed the power of this prime in either the factorization of a or that of b, Further, no larger integer can divide both a and b, because the exponents of the primes in this factorization cannot be increased, and no other primes can be included.

EXAMPLE 14 Since the prime factorizations of 120 and 500 are 120 = 23 - 3 - 5 and 500 = 22 53, the
greatest common divisor is

gcd(120,500) = 2 in(3,2)3 min(1, 0)5 min(1, 3) = 2 2 3051 = 20.

Prime factorizations can also be used to find the least common multiple of two
integers.

DEFINITION 7 The least common multiple of the positive integers a,and b is the smallest positive
integer that is divisible by both a and b. The least common multiple of a and b is
denoted by lcm(a, b).

least common multiple exists because the set of integers divisible by both a and b
is nonempty, and every nonempty set of positive integers has a least element (by the
well-ordering property,,which will be discussed in Section 3.3). Suppose that the prime
factorizations of a and b are as before. Then the least common multiple of a and b is
given by

pmax(al,bl) nax(a2,bD ... tnax(a_ b,,)

lcm (a, b) 1 ~2 Piz

where max(x, y) denotes the maximum of the two numbers x and y. This formula is valid since a common multiple of a and b has at least max(ai, bi) factors of pi in its prime factorization, and the least common multiple has no other prime factors besides those in a and b.

3 5 2 4 39
EXAMPLE15 What is the least common multiple of 2 3 7 and 2 3

Solution: We have

2 4 max(3,4 max(5,3 max(2,O) 4 5 2

lcm(2'3'7 , 2 3') = 2 )3 )7 2 3 7

The following theorem gives the relationship between the greatest common divisor and least common multiple of two integers. It can be proved using the formulae we have derived for these quantities. The proof of this theorem is left as an exercise for the reader.

THEOREM 7 Let aan~d b be'posi6e integers. err,

ab.=. gcd(a, b) lcm(a, b).

SOME USEFUL RESULTS

An important result we will use throughout this section is that the greatest common divisor of two integers!a and b can be expressed in the form

sa + tb

where s and t are integers. In other words, gcd(a. b) can be expressed as a linear combination with integer coefficients of a and b. For example, gcd(6, 14), = 2, and 2 = (-2) 6 + I - 14. We state this fact as Theorem 1.

THEOREM1 If a and b are positive integers. then there exist integers a and t such that gcd(a, b)

so + to.

We will not give a formal proof of Theorem I here (see Exercise 66 in Section 3. arid
[Ro00j for proofs), but we will provide an example of a method for finding a linear
combination of two integers equal to their greatest common divisor. (In this section. we
will assume that a linear combination has integer coefficients.) The method proceeds by
working backward through the divisions of the Euclidean algorithm. (We also descr ibe an
algorithm called the extended Euclidean algorithm that can be used to express gcd(a. b)
as a linear combination of a arid b in the preamble to Exercise 48.)

EXAMPLE1 Express gcd(252. 198) = 18 as a linear combination of 252 and 198,

Sohition: To show that gcd(252,198) = 18. the Euclidean algorithm uses these divisions:

252 = I - 198 + 54 198 = 3 - 54 + 36 54 = 1 - 36 + 18 36 = 2 - 18.

Using the next-to-last division (the third division), we can express gcd(252. 198) IS as a linear combination of 54 and 36. We find that

18 = 54 - 1 - 36.

The second division tells us that

36 = 198 - 3 - 54.

'304 Substituting I this expression for 36 into the previous equation, we can express 18 as a
linear combination of 54 and 198. We have

18 = 54 - 1 - 36 = 54 - 1 - (198 - 3 54) 454 - 1 -198.

The first division tells us that

54 252 - 1 198.

we can express 18 as a Substituting this expression for 54 into the previous equation, linear combination of 252 and 198. We conclude that

IS = 4 - (252 - 1 - 198) - I . 198 = 4 - 252 - 5 - 198.

completing the solution. everal useful results. One of our a als will be

We will use Theorem I to develop s
to prove the part of the Fundamental Theorem of Arithmetic asserting that a positive
integer has at most one I prime factorization. We will show that if a positive integer has a
factorization into primes, where the primes are written in nondecreasing order, then this
factorization is unique.

First, we need to develop some results about divisibility.

LEMMA1 If a, b and c are positive integers such that gcd(a, b) I and a bc, then a c.

Proof. Since gcd(a, b) = 1, by Theorem I there are integers s and t such that

sa + tb =: I

Multiplying both sides of this equation by c, we obtain

sac + tbc == c.

Using Theorem I of Section 2.4, we can use this last equation to show that a I c. By part 2 of that theorem, a J tbc. Since a I sac and a I tbc, by part 1 of that theoreirt, we conclude that a divides sac + tbc, and hence a I c. This finishes the proof.

We will use the following generalization of Lemma I in the proof of uniqueness of

C~ t__ cise in Section 3.3, since it

prime factorizations. (The proof of Lemma 2 is left as an exer
can be most easily carried out using the method of mathematical induction, which will be
covered in that section.)

LEM" 2 if p is a prime and -p -A ~aj a2. a,, where each ai is an 'integer, then p aj. for
some

We can now show that a factorization of an integer into primes is unique. That is, we
will show that every integer can be written as the product of primes in nondecreasing
order in at most one way. This is part of the Fundamental Theorem of Arithmetic. We will
prove the other part, that every integer has a factorization into primes, in Section 3.3.

the prime factorization of a positive inte-
Proof (of the uniqueness of
ger): We will use a proof by contradiction. Suppose that the positive integer n can be writ-

ten as the product of primes in two different ways, say, n = P I P2 * ps and n = q I q2 ... qj,
each pi and qj are primes such that p I <_ P2 :!~- - - - < p. and q I q2 <_ - - - <_ qt -

When we remove all common primes from the two factorizations, we have

PilPi2 ... Pi- =: qjl qj2 * * * qj,

where no prime occurs on both sides of this equation a-nd u and v are positive integers.
By Lemma 1 it follows that pi, divides qj,, for some k. Since no prime divides another
prime, this is impossible. Consequently, there can be at most one factorization of 11 into
primes in nondecreasing order. <

Lemma I can also be used to prove a result about dividing both sides of a congru-
ence by the same integer. We have shown (Theorem 10 in Section 2.4) that we can ' mul-
tiply both sides of a congruence by the same integer. However, dividing both sides of
a congruence by an integer does not always produce a valid congruence, as Example 2
shows.

EXAMPLE2 The congruence 14 =_ 8 (mod 6) holds, but both sides of this congruence cannot be divided

by 2 since 14/2 = 7 and 8/24, but 7 # 4 (mod 6).

-4

However, using Lemma 1, we can show that we can divide both sides of a congruence by an integer relatively prime tojhe modulus. This is stated as Theorem 2.

THEOREM 2 Let in be a positive integer and let a, b, and c be integers. If ac =_ bc'('mod in) and
gcd(c, in) = 1, then a =_ b (mod in).

Proof Since ac =_ bc (mod in), in I ac - bc = c(a - b). By Lemma 1, since
gcd(c, in) = 1, it follows that in I a - b. We conclude that a _= b (mod in).