ชีวะ

การเจริญเติบโตและการสูญสลาย ( สมการเชิงเส้น)

ปัญหาค่าเริ่มต้น 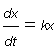; 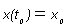โดยที่ k เป็นค่าคงที่ของการ เพิ่มหรือ ลด ซึ่งสามารถหาได้ ทั้งของการเจริญเติบ และการสูญสลาย เช่นการเจริญเติบโตของประชากร ( เช่น แบคทีเรีย หรือ สัตร์ขนาดเล็กๆ
ในช่วงเวลาสั้นๆ เวลาหนึ่ง ถ้าเรารู้ จำนวนประชากรที่เวลาเริ่มต้น ให้เป็นเวลา t = 0 เราสามารถใช้สมการ
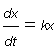เพื่อทำนายจำนวนประชากรในอนาคตได้ ( เมื่อเวลา t > 0 )
ในวิชาฟิสิกส์ ปัญหาค่าเริ่มต้น ดังสมการ 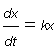สร้างโมเดล ในการประมาณปริมาณ ที่หลงเหลืออยู่ของสสาร ที่ถูกแบ่งแยก สูญสลาย จนกระทั่ง การแพร่รังสี เช่นเดียวกัน สมการเชิงอนุพันธ์ 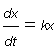สามารถใช้คำนวนการเย็นลงของร่างการ ในวิชาเคมี ปริมาณของสารที่เหลือจากปฏิกิริยาหนึ่งๆ ก็สามารถอธิบายได้โดย สมการ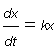
ค่าคงที่ k สามารถหาได้โดย การแทนที่ x ที่เวลา t1>t0 โดยที่
ค่าคงที่ของการเพิ่มขึ้นจะมี k >0
ค่าคงที่ของการลดลงจะมี k<0

Example ที่เวลาเริ่มต้น แบคทีเรียมีจำนวน N ที่เวลา t = 1 ชั่วโมง จำนวนแบคทีเรียเป็น 3/2N ถ้าอัตราการเติบโตเป็นสัดส่วนกับจำนวนปัจจุบัน จงคำนวนหาเวลาที่ทำให้ แบคทีเรียมีจำนวนเป็น 3 เท่า

Solution
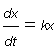โดย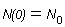
จะพบว่าสมการ --->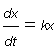

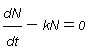
เป็นสมการ separable และเชิงเส้น
ใช้ integrating factor 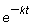คูณทั้งสองข้าง ได้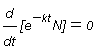
อินทิเกรตทั้งสองข้าง ได้สมการสุดท้าย และผลเฉลยทั่วไปเป็น

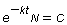หรือ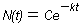
ที่ t = 0 ได้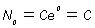
เพราะฉนั้น 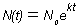ที่ t = 1 N = 3/2N ---> จะได้ k = ln3/2 = 0.4055 ดังนั้นจะได้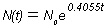
หาเวลาที่ทำให้แบคทีเรียมีจำนวนเป็น 3 เท่า --->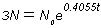
จะได้ t = 2.71 Ans

แบบฝึกหัด

1).การเติบโตของแบคทีเรียจะเติบโตโดยได้สัดส่วนพอดีกับปริมาณอาหารและพื้นที่ ในแรกเริ่มมีแบคทีเรีย 250 แล้วหลังจากนั้น 7 ชั่วโมงมีแบคทีเรีย 800 ได้จากกการเพาะ จงหาค่าประมาณเป็นตัวเลขของการเพาะพันธุ์แบคทีเรีย ณ เวลา t ใด ๆ

2).การเติบโตของแบคทีเรีย จะเป็นอัตราส่วนคงที่เป็นจำนวนตัวเลข พบว่าจะเป็นจำนวนสองเท่าภายในเวลา 4h จงหาว่าจำนวนจะเพิ่มเป็นเท่าใดในเวลา 4h

3).ในการเพาะเชื้อยีสต์ จำนวนที่ได้จากการหมักเชื้อในอัตราส่วนจากจำนวนที่มีอยู่ ถ้าจำนวนเพิ่มเป็น 2 เท่าใน 1h จงหาว่าจะใช้เวลาเท่าใดจากจำนวนแรกเริ่มจนถึงเวลาสิ้นสุดที่ 11/4 h